what should you do if your suppose to add two percentages

Most People Spiral Up Multiple Percent Changes. Hither's How to Get Them Correct.
Solving a Common Math Problem with Everyday Applications
Incredibly, later 16 years of schooling, the bulk of American higher students get this question wrong:
What is the total percentage change in the following state of affairs?
Decrease of twoscore% followed by an increase of 60%.
A. Increase of ten%
B. Increase of 20%
C. Decrease of 4%
D. None of the to a higher place.
The reply, of course, is C, an overall decrease of 4%. Non only did the majority of college students go this question incorrect, they did non fifty-fifty get the correct direction, with over one-half guessing this was an increase. The common error is taking the percentages at face value and adding them together to get the overall percentage modify. We thus take another entry in the long list of things people aren't very practiced at, combining multiple per centum changes.
Far from existence an abstruse, theoretical idea, finding a total alter from a sequence of percentage moves has implications in our daily lives from the price of consumer appurtenances to national budgets to our retirement account value, to the battery life on our newest laptop. However, despite the ubiquity of the error and the ramifications for us personally and as a nation, we are incapable of teaching people how to correctly stack percentages. In this article, we'll discuss what the error is, how to avoid it, why this matter, and why people make it. Our primary resource is the paper: "When Two Plus Two Is Not Equal to 4: Errors in Processing Multiple Percentage Changes" (link).
What's the Problem?
The error is that when we come across two sequent percentage changes, nosotros instinctively take them at face value and add them together to get a total alter. Thus, a discount of fifty% followed by a discount of 25% is interpreted equally 75%. In equation class, for two percentages A and B, the mistake is:

The trouble is a percentage is calculated from a specific base value. After the first percentage modify, the base changes, and the second percentage does not have the aforementioned base. Two percentages that have different base values cannot be directly combined by addition! Instead, we have to work out the percentage changes separately.
How to Avert the Error when Combining Percent Changes
Offset, calculate the new base from the first percent change, then, using the new base, calculate the per centum change from the 2nd. The overall percent alter can and so be calculated from the new value and the original base value. In equation form, the overall percentage modify is:
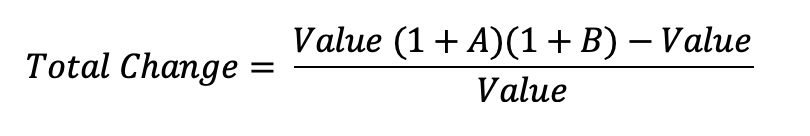
Canceling out the value yields the simpler equation for total percent alter from 2 sequential percentage changes A and B:
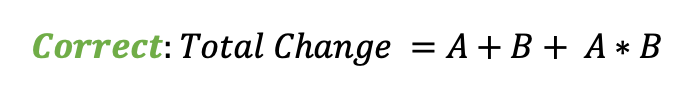
The error is in the actress term on the terminate, A * B. The fortunate part of the mistake is it always occurs in a systematic direction:
- For 2 increases, nosotros underestimate the overall percentage increase
- For ii decreases, nosotros overestimate the total pct subtract
- For 1 increase and 1 decrease resulting in an overall increase, we overestimate the total percentage increase
- For 1 increase and 1 decrease resulting in an overall subtract, nosotros underestimate the total per centum decrease
Allow'south work through examples representing these four situations:
- 2 increases: suppose the battery life of a smartphone goes up 40% in one year and 10% in the next. What's the total change?
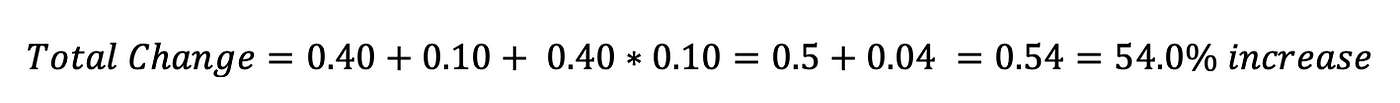
2. 2 decreases: suppose the town tax rate decreases by threescore% and then by 40% (nosotros tin can only wish). If we add the 2 together, we pay 0% tax but surely that can't be right! Indeed it isn't:
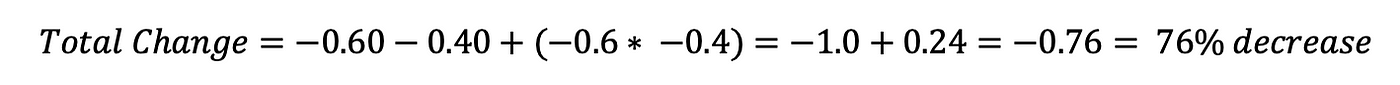
iii. 1 increase and 1 subtract resulting in an overall increment. Suppose national spending increases by 80% one yr and then decreases past forty% the next. What's the total change?
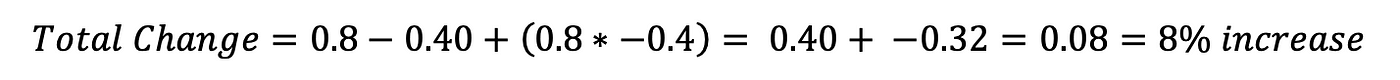
Notice that the club of the changes does non matter. We could decrease get-go and so increase, but the overall magnitude of the change is the aforementioned. If you don't believe me, start with spending of $100. The showtime order works out:

The decrease followed past the increase gives the same answer:
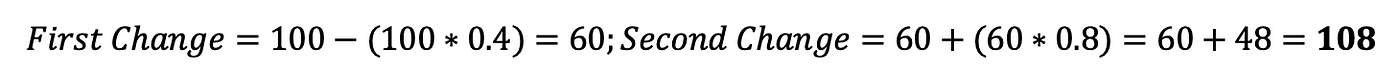
iv. 1 increment and i decrease resulting in an overall decrease. Suppose the length of a blog post increases past 60% during the starting time edit and decreases by forty% during the second (this is the same state of affairs as the initial question). Did the post get longer?
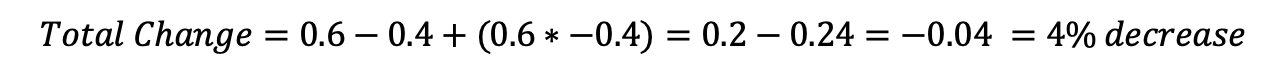
In the last instance, adding the two percentages gets yous a 20% increase in what was actually a iv% subtract. Had you made the common error, you would accept ended up on the wrong side of 0! A similar fault occurred when standardized test scores in California decreased past sixty% one year and increased by 72% the side by side, resulting in praise for the raising of student scores from the baseline. Not to be a downer, simply the full overall modify — wait, work this one out yourself — was a 31% decrease in test scores. Students were worse than 2 years previous not better, and their parents were still math illiterate (but not you anymore!).
Why Does this matter?
All of the above were hypothetical examples of very real situations. Knowingly or not, we bargain with multiple percentage changes all the time and when we don't realize this, it'due south commonly to our detriment. As with near other human errors, in that location are people already taking advantage of it for their benefit. (It'southward a good rule of thumb that errors in human logic are discovered showtime in marketing and just afterwards are they published in academic journals. For more on this, read Influence past Robert Cialdini. )
For example, look at the "double discount". This occurs oft in retail where you can take an extra 25% off an item on sale for fifty% off. The salesperson wants you to add the percentages and conclude the discount is 75% instead of the more than modest 62.5% discount for the bodily value. Or consider a computer with a brandish that has twenty% more than pixels than the terminal model which had 30% more the previous. Instead of presenting these increases separately — where adding gets you to 50% — the seller would be improve off presenting them every bit one number, 56%, which is the actual increase.
What the salesperson would be doing in these situations is framing: presenting information in a context to get u.s. to brand a determination in her favor. Any piece of data can exist presented in multiple ways — for example, a medication can exist described as having x% chance of causing a side outcome or as having a 90% chance of causing no side furnishings (the framing here is positive versus negative). Multiple percent changes are just one instance of framing, which has a profound impact on our choices (read well-nigh framing in "The Framing of Decisions" by Tversky and Kahnemann).
One of the studies in the paper "When Two Plus 2" looked at the effect of in a retail setting of presenting a discount as a single decrease or two percentage discounts. Not surprisingly, the double discount generated more than purchases, more revenue, and more profit than the equivalent single discount. While this was only a single study, the prevalence of double discounts in stores is potent testify marketers had already figured out and were using this cognitive shortcoming.
A basic principle is when nosotros refuse to practise the math ourselves, we will exist fooled by someone who has washed it.
Why Does This Happen?
1 theory that explains why nosotros are bad at percentages — as well as fractions and decimals — is that humans evolved math skills only dealing with whole numbers. "Whole number say-so" makes sense from an evolutionary standpoint: things in nature really only come in whole numbers. We're never chased past 1.7 mount lions or must take ii.five children to behave on the species. Over millions of years, we got pretty good at adding together whole numbers. In more than complex situations — calculating the compound percentage return on your retirement account — our evolved abilities don't concur up well.
I think the mistake in computing percent changes is a combination of our predilection for whole numbers and remaining in system one thinking. If y'all've read works like "Thinking, Fast and Dull", then you are familiar with the concept of the two systems of thinking. The first is a quick, instinctual judgment made using a ready of heuristics and biases (mental shortcuts). The second way is a prolonged, rational decision made past reasoning through multiple pieces of information. The beginning system works well for situations our ancestors encountered merely breaks down in information-rich, constantly changing environments, exactly where nosotros find ourselves now.
Calculating the total effect of multiple percent changes requires switching from ane to two which is effortful and something we endeavor to avoid. Unfortunately, system 1 seems incapable of multiplication and takes a shortcut — add-on — to summate that a 50% and 25% increment is 75% instead of 87.v%.
Some other of the studies in "When Two Plus Two" looked at when we do the multiple percent calculation correctly. Interestingly, they found we unconsciously make an effort vs payoff tradeoff and simply stop to calculate the correct answer when the payoff is worthwhile (for this study, a couple of dollars for the right solution). We should be careful about extrapolating from a single study, but external rewards (sometimes) motivate us to work harder.
Similarly, when the pct changes were easy to compute, say a 20% decrease and a 10% decrease (total of eighteen% decrease), the error rate went down. Thus, either lowering the effort or increasing the payoff seems to result in more than accurate calculations. The third state of affairs where the error rate decreased was when the total from adding percentages was conspicuously not possible, equally with discounts of 80% and 40%. People know that the price of a product cannot decrease by 120% or they would accept to be paid to buy information technology!
In summary, nosotros incorrectly calculate multiple percentage changes considering it requires effort to reason through the right answer. We are good at adding and using whole numbers, merely not then good with multiplication and percentages. The solution is just every bit straightforward every bit the problem: accept the time to carry out calculations for yourself instead of assuming the reply. Virtually important decisions in our world requiring recruiting organization 2, so you lot might as well train it at every opportunity!
Conclusions
The multiple per centum alter mistake occurs when we take percentages at face up value and add them together. The correct approach is to carry out the calculations separately or use the right formula:
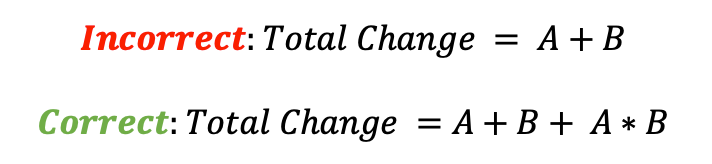
Applying the right equation volition let you see that double discounts are not every bit large equally they seem, double increases are larger than they announced, and to make upward for a lx% decrease requires not a 60% increment, but a 150% increase!
Yes, it may take a niggling more than effort, but when you are not willing to do the math yourself, information technology means you volition lose out to those who do. I hope that even if your self-confidence took a 40% hit at the beginning of this article, it has since increased by 90% to come out 14% positive.
As e'er, I welcome feedback and constructive criticism. The best identify to reach me is on Twitter @koehrsen_will.
Source: https://towardsdatascience.com/most-people-screw-up-multiple-percent-changes-heres-how-to-do-get-them-right-b86bd6ef4b72
0 Response to "what should you do if your suppose to add two percentages"
Publicar un comentario